Ki-kare analizi online uygulama (hesaplama) aracı

Ki-kare analizi nedir?

Ki-kare analizi, gözlenen ve beklenen veriler arasındaki farkı belirlemek için kullanılan bir istatistiksel prosedürdür. Parametrik olmayan bir test olduğundan verilerin normal dağılım varsayımını karşılaması gerekmez. Ki-kare analizi, iki kategorik değişken arasındaki ilişkiyi test etmek veya bir örneklem dağılımının teorik bir dağılıma uyup uymadığını test etmek için yaygın olarak kullanılır.

Ki-kare bağımsızlık testi

Ki-kare bağımsızlık testi, iki kategorik değişkenin birbirinden bağımsız olup olmadığını test etmek için kullanılır. Bu, bir değişkenin dağılımının diğer değişkenin dağılımından etkilenmemesi anlamına gelir.

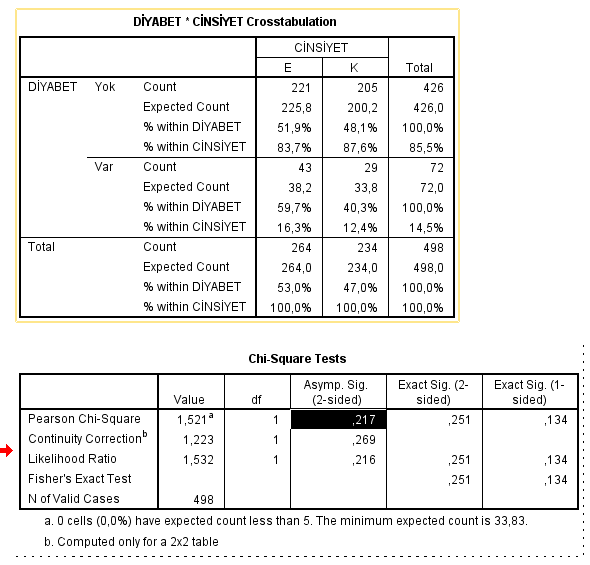
Ki-kare bağımsızlık testini gerçekleştirmek için araştırmacı bir olasılık/çaprazlama (contingency) tablosu oluşturur. Olasılık (veya çaprazlama) tablosu, iki kategorik değişkenin çapraz karşılaştırılmasını gösteren bir tablodur (cross-tabulation). Tablonun satırları ve sütunları iki değişkenin farklı kategorilerini temsil eder ve tablonun hücreleri her kategori kombinasyonu için gözlenen sayıları içerir.

Çaprazlama tablosu her hücre için beklenen sayılar, iki değişkenin bağımsız olduğu varsayımı altında hesaplanır. Ardından, gözlenen sayılar beklenen sayılarla karşılaştırılarak ki-kare istatistiği hesaplanır.

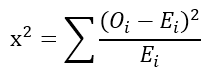
Ki-kare istatistiği (X² değeri) büyük ve p-değeri tanımlanmış değerden küçükse (medikal alanda p<0,05 baz alınır), araştırmacı bağımsızlık için sıfır hipotezini reddedebilir ve iki değişken arasında önemli bir ilişki olduğu sonucuna varabilir. Sıfır hipotezi (H₀) reddedildiğinde ana hipotez (H₁) kabul edilir ve gruplar arasında anlamlı dağılım (veya çaprazlama) ilişkisi olduğu yorumu yapılır.

Ki-kare uygunluk testi (goodness-of-fit test)

Ki-kare iyi uygunluk testi, bir örneklem dağılımının teorik bir dağılıma uyup uymadığını test etmek için kullanılır. Örneğin, bir araştırmacı bir madeni paranın atılması örneğinin binom dağılımını takip edip etmediğini test etmek için ki-kare iyi uygunluk testini kullanabilir.

Ki-kare analizi uygulama alanları ve hipotezler

Ki-kare analizi, çok çeşitli bilimsel uygulamalarda kullanılabilen çok yönlü bir istatistiksel araçtır. Bazı örnekler şunlardır:

• Yeni bir ilacın bir hastalığı tedavi etmede etkili olup olmadığını test etme
• Yeni bir eğitim programının öğrenci başarısını artırmada etkili olup olmadığını test etme
• Belirli bir çevresel toksine maruz kalma ile belirli bir kanser türü arasında bir ilişki olup olmadığını test etme
• Belirli bir genetik mutasyonun belirli bir hastalıkla ilişkili olup olmadığını test etme
• Belirli bir pazarlama kampanyasının satışları artırmada etkili olup olmadığını test etme
• Belirli bir sosyal medya platformunun siyasi bilinç düzeyini artırmada etkili olup olmadığını test etme

Ki-kare analizi, bilimsel araştırmalar için güçlü bir araçtır, ancak dikkatli kullanmak ve sınırlarını anlamak önemlidir. Örneğin, ki-kare testi bir nedensellik testi değildir. Bir ki-kare testi, iki değişken arasında önemli bir ilişki ortaya koyarsa, bu mutlaka bir değişkenin diğerine neden olduğu anlamına gelmez. İki değişken arasındaki ilişkiyi açıklayabilecek diğer faktörleri her zaman göz önünde bulundurmak önemlidir.

Ek olarak, ki-kare testi örneklem boyutuna duyarlı olabilir. Örneklem boyutu çok küçükse, test iki değişken arasında önemli bir ilişkiyi tespit edemeyebilir, hatta varsa bile. Tersine, örneklem boyutu çok büyükse, test iki değişken arasında anlamlı olmasa bile önemli bir ilişki tespit edebilir.

Sonuç olarak, ki-kare analizi, kategorik değişkenler arasındaki ilişkilerle ilgili hipotezleri test etmek isteyen bilimciler için değerli

Ki-kare analizi test uygulanabilirlik varsayımları

• Her iki değişken de kategorik olmalıdır. Bu, değişkenlerin nominal veya ordinal ölçüm seviyesinde ölçüldüğü anlamına gelir. Nominal değişkenler, cinsiyet veya saç rengi gibi kategorilerin yalnızca farklı adlar olduğu değişkenlerdir. Ordinal değişkenler ise eğitim seviyesi veya müşteri memnuniyeti gibi kategorilerin doğal bir sıraya sahip olduğu (sıralama niteliğindeki) değişkenlerdir.
• Tüm gözlemler bağımsız olmalıdır. Bu, her gözlemin örneklemdeki gözlemsel parametrelerle ilişkili olmadığı anlamına gelir.
• Contingency (çaprazlama) tablosundaki hücreler birbirini dışlayacak şekilde olmalıdır. Bu, her gözlemin yalnızca contingency tablosunun (çaprazlama tablosu) bir hücresine düşmesi gerektiği anlamına gelir.
• Hücrelerin beklenen değeri, hücrelerin en az %80’inde 5 veya daha büyük olmalıdır. Yüzde yirminin (>%20) üzerinde hücrede beklenen değer 5’ten küçük olarak görüldü ise (expected count), bunun yerine Fisher’s exact testi gibi alternatif analizler kullanılmalıdır.

Bu varsayımlardan herhangi biri ihlal edilirse, Ki-kare testinin sonuçları güvenilir olmayabilir. Verinizi analiz etmek için kullanmadan önce Ki-kare testinin varsayımlarını kontrol etmek önemlidir.

Ki-kare testini kullanırken aklınızda bulundurmanız gereken bazı ek hususlar şunlardır:

• Ki-kare testi, iki kategorik değişken arasında bağımsızlık olup olmadığını test etmek veya bir kategorik değişken ile teorik bir dağılım arasında uygunluk testini test etmek için kullanılabilir.
• Ki-kare testi yönlendirme içermeyen bir testtir, yani size iki değişken arasındaki ilişkinin yönünü söyleyemez. Eğer ilişkinin yönü ile ilgileniyorsanız, Cramer’s V veya Phi katsayısı gibi farklı bir istatistiksel test kullanabilirsiniz.
• Ki-kare testi güçlü bir istatistiksel testtir, ancak doğru kullanmak önemlidir. Ki-kare testini nasıl kullanacağınızdan emin değilseniz, her zaman bir istatistikçiye danışmanız en iyisidir. Yanlış kullanımlar istatistisekl sonuçlarınızın yanlış olması ve yanlış yorumlanmasına neden olabilir.

Ki-kare analizi ve tanımlar

Ki-kare (X² değeri)

Ki-kare (X²) değeri gözlenen ve beklenen frekanslar arasındaki farkı ölçmek için kullanılan istatistiksel bir test istatistiğidir. Çaprazlama tablosunda gözlenen ve beklenen sayılar arasındaki karelenmiş farkların toplamının beklenen sayılara bölünmesiyle hesaplanır.

Ki-kare değeri, gözlenen ve beklenen frekanslar arasındaki genel uygunluğun bir ölçüsüdür. Ki-kare değeri küçükse, gözlenen ve beklenen frekanslar birbirine benzerdir ve gözlenen ve beklenen frekanslar arasında fark olmadığına ilişkin sıfır hipotezi desteklenir. Ki-kare değeri büyükse, gözlenen ve beklenen frekanslar farklıdır ve sıfır hipotezi reddedilmesi yönünde desteklenir. P anlamlılık değeri X² (ki-kare değeri) ile desteklenerek yorum yapılır.

P anlamlılık değeri

Kısaca P değeri anlamlılık değeridir ve H₀ hipotezinin reddedilip reddedilmeyeceğine karar vermeye yarar. H₀ (yokluk hipotezi) reddedilirse, H₁ hipotezi kabul edilir ve anlamlı istatistiksel dağılım farklılığı vardır şeklinde yorum yapılır. Tıp alanında tip 1 hata değeri genellikle %5 kabul edildiğinden, p<0,05 anlamlılık sınırı olarak kabul görür.

Serbestlik derecesi (df)

İstatistikte serbestlik dereceleri (df), bir istatistiksel analizde bağımsız değerlerin sayısıdır. Gözlemlerin sayısından gözlemler üzerindeki kısıtlamaların sayısının çıkarılmasıyla hesaplanır.

Serbestlik dereceleri önemlidir çünkü istatistiksel hipotezleri test etmek için kullanılan olasılık dağılımının şeklini belirlerler. Örneğin, ki-kare testi bir ki-kare dağılımı kullanır ve t-testi bir t-dağılımı kullanır. Bu dağılımların şekli serbestlik derecelerine bağlıdır.

Belirli bir istatistiksel test için serbestlik dereceleri, teste bağlı olarak farklı şekilde hesaplanır. Örneğin, ki-kare bağımsızlık testinin serbestlik dereceleri aşağıdaki şekilde hesaplanır:

df = (r - 1)(c - 1)

Burada r tabloda satır sayısı ve c tabloda sütun sayısıdır.
Örneğin 2×2’lik bir ki-kare analizinde serbestlik derecesi (2-1)*(2-1) = 1 (df) şeklinde hesaplanır. 3×3’lük bir çaprazlamada ise serbestlik derecesi ise (3-1)*(3-1)=4 (df) şeklindedir.

Ki-Kare analizinde Yates düzeltmesi nedir ve nasıl kullanılır?

Yates düzeltmesi, örneklem boyutları küçük olduğunda ki-kare testlerinde hata ve sapmaları azaltmak için kullanılan bir istatistiksel yöntemdir. 1930’larda ilk olarak düzeltmeyi öneren İngiliz istatistikçi Frank Yates’in adını almıştır.

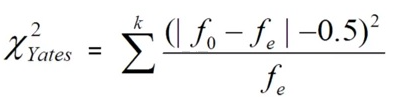
Yates düzeltmesi, ki-kare istatistiğini hesaplamadan önce tabloda gözlenen her sayımdan 0,5 çıkararak gerçekleştirilir. Örneklem boyutları küçük olduğunda, ki-kare dağılımında sapma ve hatalar (abartılı anlamlılık düzeyleri) görülebilir; bu da tip I hata (yanlış pozitif) riskinin artmasına neden olabilir. Bu bağlamda örneklem sayısının kısıtlı olduğu analizlerde tip 1 hata (alfa) oranını azalmak adına tercih edilebilir.

Yates düzeltmesi, bağımsızlık ki-kare testlerinde örneklem boyutları küçük olduğunda kullanılmalıdır. Genel kural olarak, tablodaki beklenen değer herhangi bir hücrede 5’den az ise Yates düzeltmesini tercih edilebilir.

Sonuç olarak kısıtlı örneklem sayılarında Yates p değeri dikkate alınmalıyken örneklem sayısının fazla olduğu analizlerde kullanımına gerek yoktur. Yeterli örneklem sayılarının olduğu analizlerde doğrudan Pearson ki-kare analizinin p değeri dikkate alınabilir. Şunu da belirtmek gerekir ki kısıtlı örneklem sayılarının olduğu durumlarda Yates düzeltmesinin alternatifi olan Fisher’s exact testi daha uygun ve güçlü bir metodu kullanmak da iyi bir seçenek olabilir. Bu kavramların değerlendirilmesi ve tercihi istatistiksel bilgi ve tecrübe gerektirdiğinden özellikli durumlarda, eğer emin değilseniz bir istatistikçi ile görüşerek daha profesyonel bir destek almanız uygun olacaktır. Aracımızda hem Pearson ki-kare analizinden elde edilen p değeri, hem de Yates düzeltmesinden elde edilen p değeri kullanımınıza sunulmuştur.

Uzm. Dr. F. İkiz